Алгоритм Беллмана-Форда предназначен для поиска коротких путей в направленном графе, который может содержать отрицательные веса. Алгоритм был разработан в 1950-х годах Ричардом Беллманом и Лестером Фордом независимо друг от друга.
Основные идеи алгоритма
Алгоритм Беллмана-Форда расслабляет ребра графа, начиная с определенной начальной вершины. Это означает, что если расстояние до конечной вершины данной пимпы может быть уменьшено путем перемещения из текущей вершины, то это проверяется на каждой итерации пимпы. Если это возможно, расстояние обновляется.
Выполните ровно V-1 повторений, где V — количество вершин графа. На каждой итерации все ребра графа «расслабляются». Таким образом, алгоритм имеет вычислительную сложность o(ve), где e — количество ребер.
Преимущества и недостатки
Основными преимуществами алгоритма Беллмана-Форда являются

Пошаговая работа алгоритма

Рассмотрим алгоритм Беллмана-Форда на простом примере.
Ниже представлен исходный граф с пимпловскими весами и вершиной S в качестве источников. Итерационная работа пошагового алгоритма показана ниже.
Как видно из примера, алгоритм очень прост, но эффективно находит все короткие пути из конкретной вершины после V-1 итераций.
Алгоритм Беллмана-Форда для параллельных вычислений
Как и многие другие алгоритмы на графе, алгоритм Беллмана-Форда имеет возможность вычисления подобий.
Таким образом, при наличии o(e) параллельных вычислительных устройств высота параллельной формы алгоритма Беллмана-Форда может быть сведена к O(d) где D — диаметр графа.

Применение алгоритма на практике
Например, алгоритм Беллмана-Форда используется очень часто, хотя его сравнивают с тем же алгоритмом Дейкстры, хотя и с той же простотой и асимптотической сложностью.
Таким образом, алгоритм Беллмана-Форда активно используется для решения реальных оптимизационных задач, несмотря на его очевидный академический характер.
Применение алгоритма Беллмана-Форда
Рассмотрим проблемы, связанные с реализацией этого алгоритма в программном обеспечении. В целом, алгоритм очень прост и легко программируется на различных языках программирования.
Обобщение и модификация
Существует несколько обобщений и модификаций классического алгоритма Беллмана-Форда.
Развитие идей: комбинированные алгоритмы
Очень перспективным направлением является разработка комбинированного алгоритма на основе алгоритмов Беллмана-Форда и Дейкстры/a*.
Этот подход сочетает в себе уникальные возможности Беллмана-Форда и скорость Дейкстры, что позволяет получить эффективный гибридный алгоритм, который можно применять к более широкому кругу задач.
Увеличение скорости алгоритма
Несмотря на простоту алгоритма Беллмана-Форда, его производительность может снижаться при работе с большими графами. Давайте рассмотрим возможные способы повышения производительности.
Уменьшить количество итераций
Как было показано ранее, алгоритм выполняет ровно V-1 итераций. Однако на практике кратчайший путь часто находится гораздо раньше.
Эффективное хранение графов
Хранение графа в виде матрицы смежности замедляет поиск ребер. Рекомендуется использовать
Программная реализация: детали и подводные камни
При практической реализации алгоритма следует обратить внимание на следующие моменты
Итоговые значения могут выходить за пределы диапазона int из-за возможного наличия отрицательных ребер. Использование лонгов является обязательным.
Обнаружение отрицательных петель
Для этого необходимо сохранить вершины, по которым распространяется улучшенное расстояние, и проверить последующий граф.
Применение устройств линейного программирования
Задача о кратчайшем пути может быть сформулирована как задача линейного программирования (ЛП).
Переменные ЛП определяют поток вдоль ребер, объективная функция — общую длину пути, а ограничения определяют поток в вершинах и ребрах.
Это позволяет использовать общие методы ЛП, такие как симплекс, внутренние точки и т. д., для поиска общего оптимума.
Применение методов искусственного интеллекта
Применение методов искусственного интеллекта для поиска кратчайших путей может иметь следующие последствия.
Такие подходы намного быстрее классических алгоритмов и дают очень адекватные результаты, а также являются приближенными.
Как работает сам алгоритм?
Он должен распознать остаточную сеть как тот же граф, что и входной, и тогда он выполняет над ней некоторые операции.
Пример из практики.
Разбейте итерации потока по выбранному пути на более мелкие шаги, чтобы представить, как меняется остаточная сеть после облегчения следующего потока.
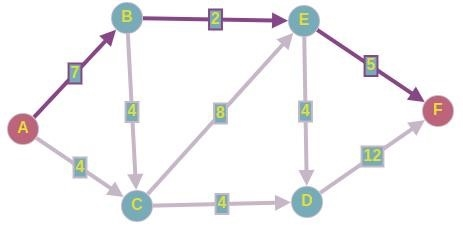
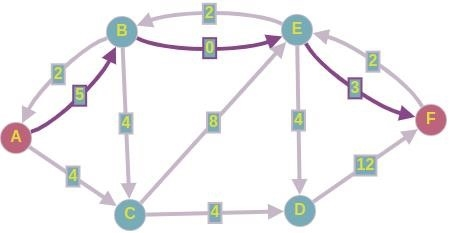
Нуль-взвешенные ребра могут быть удалены. Таким образом, на первой итерации мы смогли увеличить максимальный поток на две точки.
Теперь дело за итерациями, пока есть способ.
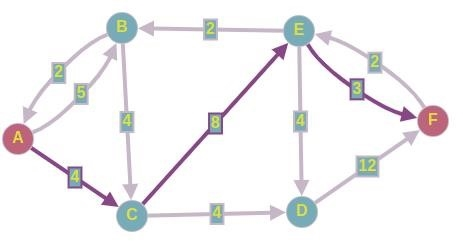
Пропускаем три точки потока по этому пути и восстанавливаем остаточную сеть. Получаем следующее.
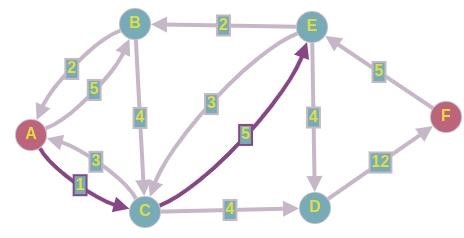
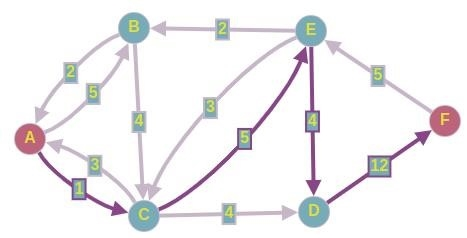
Оставьте одну единицу потока на этом пути и восстановите остаточную сеть. На экране появится следующая картина.
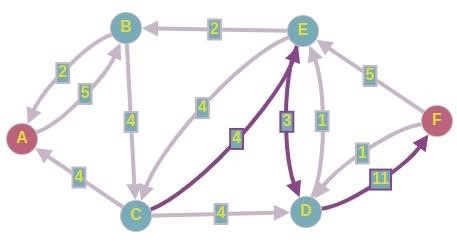
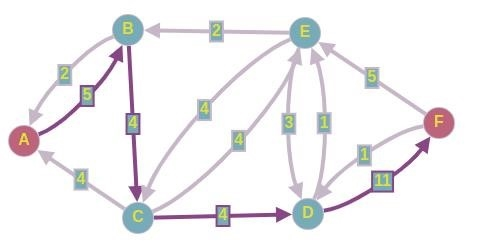
Оставьте четыре единицы потока на этом пути и восстановите остаточную сеть. На экране появится следующий рисунок.
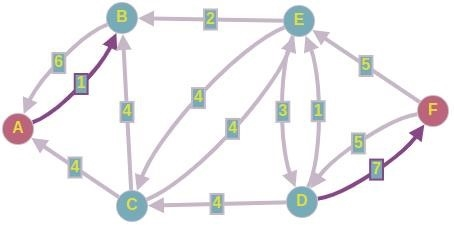
В этот момент алгоритм больше не будет работать, так как нет пути от источника к дренажу. Тогда ответом на вопрос будет сумма всех найденных потоков пути роста. Ответ — 10 единиц.
Большое спасибо, надеюсь, я вам помог! Буду рад вашим комментариям и исправлениям, чтобы сделать презентацию более доступной!
Шаг 1. Найдите букву T.
Первое, что нужно сделать, чтобы начать решать эту задачу, — заменить букву D на букву F и сразу же расшифровать вторую букву: 5 + 5 = 10, поэтому буква t = 0. Второй момент: если сумма двух цифр в одном столбце больше 10, то единица переносится на старшую цифру в числе. Также рекомендуется писать цифры от 0 до 9 в каждом столбце, где нужно расшифровать новый символ, сопоставив его с известным числом. Объясним графически, что у нас получилось:
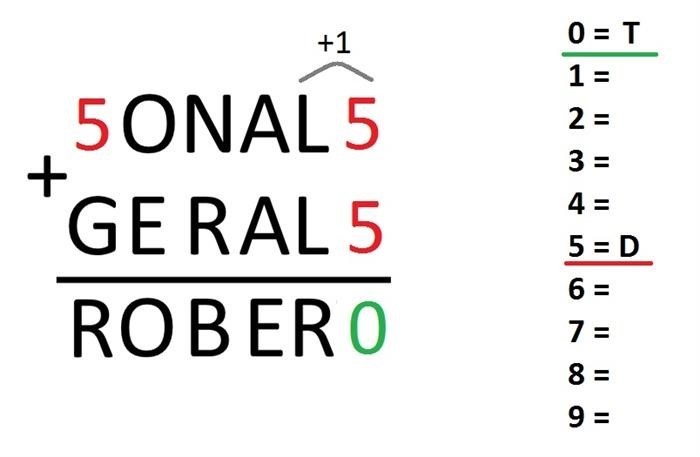
Шаг 2. Найдите букву e
После этого все становится немного сложнее… Первое, что привлекает ваш взгляд, — это второй столбец слева: o+e = o, вас ничего не смущает? Я имею в виду, что одно число равно другому… Одно и то же число? Далее вам нужно определить комбинацию чисел, которая делает эту ситуацию возможной. Если сложить только два числа, то такой эффект невозможен, но здесь ему помогает перенос +1 из предыдущего столбца n+r=b. Теперь, немного подумав, выясняется, что буква e = 9, так как «любая цифра» + 9 = «любая цифра» -1. (точнее — 1 цифра). Итак, буква e равна 9, поэтому она прибавляется к любой цифре, давая еще +1 к верхней цифре (то есть в левом столбце). Графически эта точка решения выглядит следующим образом
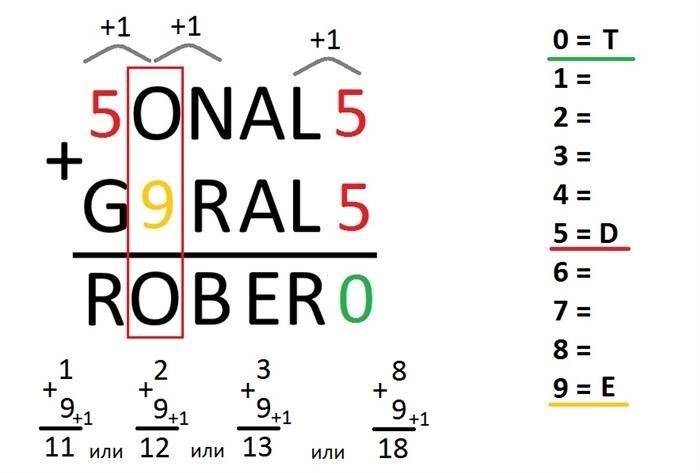
Шаг 3. Найдите буквы g и r
Три буквы известны. Решаем дальше. Согласно полученной общей информации, левый столбец является головным. Общее количество известно. Из предыдущего столбца добавляется единица, и слева нет большего числа. (См. также.) Применим метод списков, характерный для математики. Определим числа, которые можно составить для буквы g. Поскольку 0 занято буквой Т, что же еще: если вместо g поменять 3, то 5+3 = 8, добавить еще 1 из предыдущего столбца — получится r = 9, но 9 уже занято. Символ Е. Следовательно, символ g может быть либо 1, либо 2. Это связано с тем, что буква r также находится во втором столбце Весов + 1 = дисбаланс. Если g = 2. 5 + 2 + 1 = 8 — хорошее число и нам не подходит. Поэтому g равно 1. Зная, что g = 1, вычислим букву r: 5 + 1 + 1 = 7.
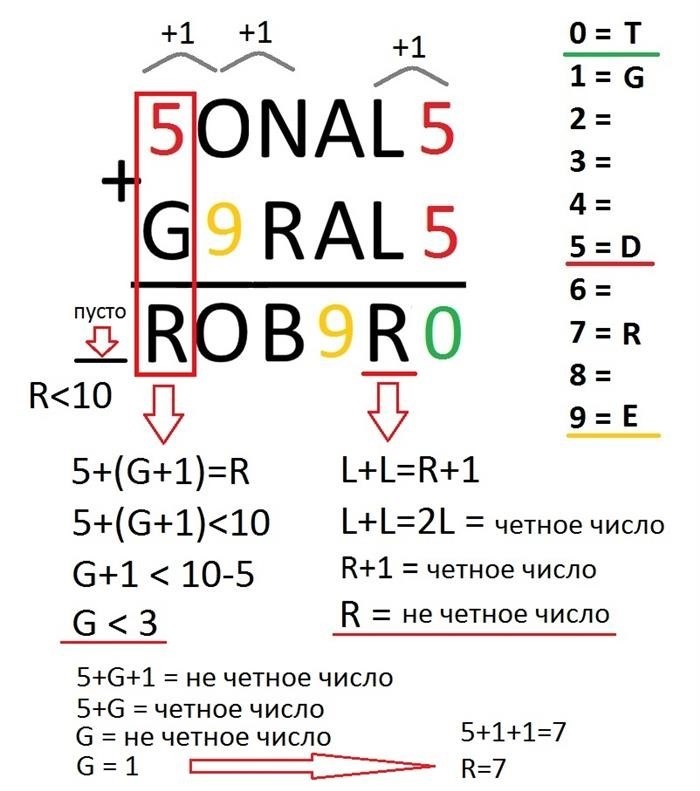
Надеемся, мы максимально подробно объяснили, как вычислить значения букв G и R. Не забудьте записать все известные числа в столбцы.
Шаг 4. Найдите буквы L и A
При решении этой задачи легко допустить ошибки, которые приведут к неправильному последующему решению и потере драгоценного времени. Некоторые люди считают, что L=3, в то время как L+L+1=7. Не торопитесь. Сначала рассмотрите соседний столбец слева, A+A=9. Рассматривая все оставшиеся варианты 2, 3, 4, 6 и 8, мы видим, что совпадений всего четыре, то есть A = 4. В этом случае нужно добавить 1 из предыдущего столбца (L+L+1=7). В результате получается L + L + 1 >. 10, то есть L + L + 1 = 17. Следовательно, можно легко вычислить L = 8. Далее следует графическое объяснение.
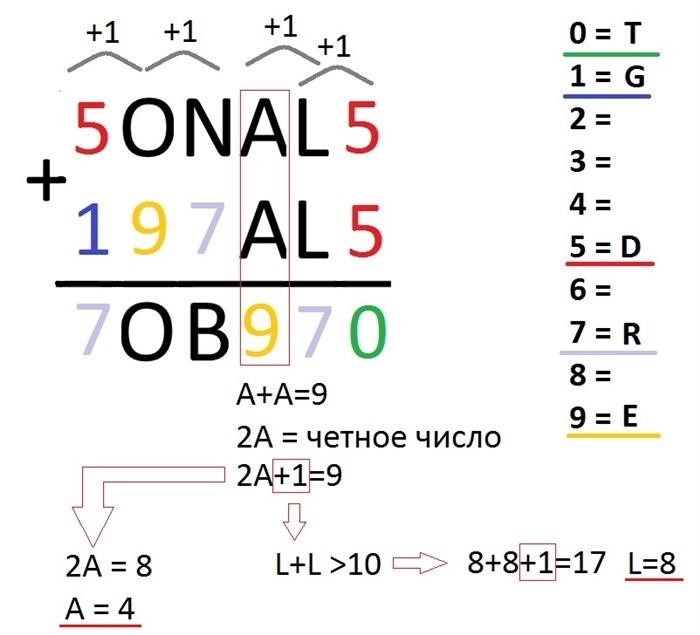
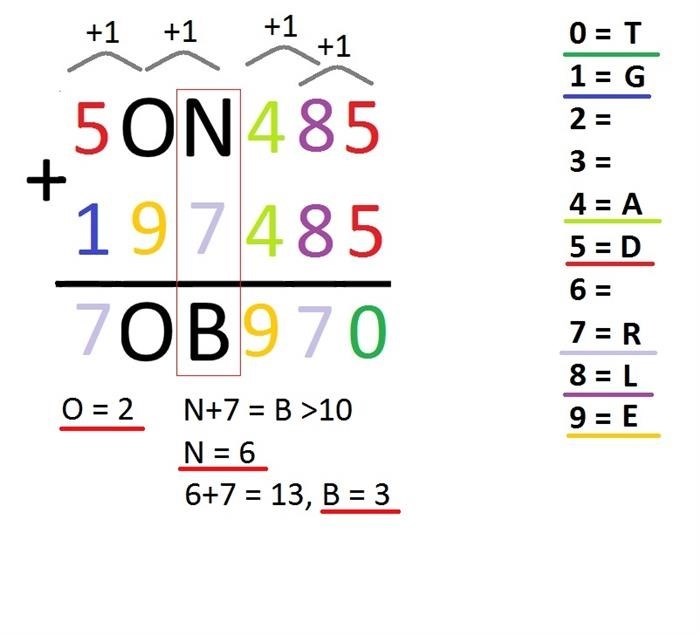
Шаг 5. Найдите оставшиеся буквы O, N и B.
Осталось всего три числа, которые не были расшифрованы: 2, 3 и 6. Рассмотрим столбец N + 7 = B. Мы видим, что сумма больше 10, потому что к следующему числу прибавляется +1. Очевидно, что N не равно ни 2, ни 3, поэтому N = 6. Следовательно, вычисляется 6+7=13, что дает B = 3. Последнее оставшееся число — 2, которое мы присваиваем букве О. Для тех, кто может визуально распознать информацию, решение показано ниже.
detector